Materi Kelas 6 B

 SELASA, 03 Januari 2023

TEMA 6 SUBTEMA 1 PB 3 DAN 4 DAN MATEMATIKA

(BANGUN RUANG  PRISMA)

MUATAN  TEMATIK DAN MATEMATIKA KELAS VI.B

GURU KELAS FITRI DARYANI,S.Pd MBJARA

Tabiik puuun.....

Good morning every body, how are you today? I wish you fine and happy today. Puji syukur marilah kita panjatkan kehadirat  Alloh SWT sehingga pada hari ini kita dapat bertemu kembali pada pembelajaran kita. Semoga kita  selalu sehat dan senantiasa dalam lindungan Alloh SWT. Anak - anak sebelum mulai pembelajaran sebaiknya kita mendengarkan tausiyah dahulu, menyanyikan lagu wajib,berdo'a sebelum belajar, melaksanakan sholat duha, dan muroja'ah surat-surat pendek. Tak lupa ibu mengingatkan, selalu laksanakan sholat wajib tepat pada waktunya. TETAP SEMANGAT

Tema  6 (Menuju Masyarakat Sejahtera)

Subtema1(Masyarakat Peduli Lingkungan)

Pembelajaran  3 & 4

Subtema               : 1(Masyarakat Peduli Lingkungan)

Pembelajaran      : 3&4

Alat Peraga          : PPT dan Video

Untuk lebih memahami materi hari ini anak Sholeh dan Sholehah bisa menyimak video hari ini ya

Demikian pembelajaran hari ini semoga anak Sholeh dan Sholehah dapat memahami materi hari ini 🙏😍

. Bangun Ruang Sisi   Datar(PRISMA)

• Kubus

Bangun Ruang Kubus

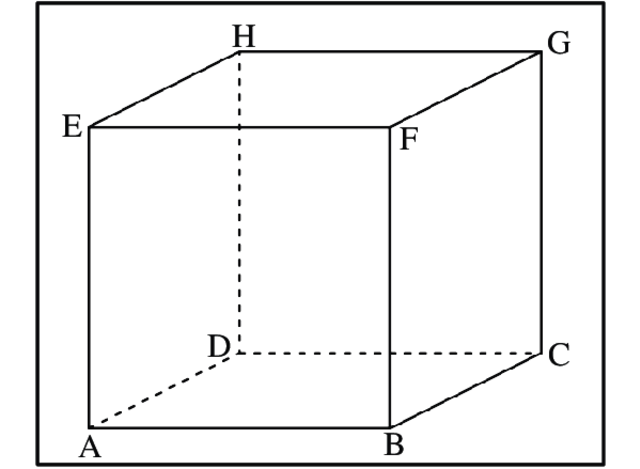
Bangun ruang kubus merupakan bangun ruang tiga dimensi yang dibatasi oleh 6 (enam) sisi yang serupa, 12 (dua belas) rusuk sama panjang dan 8 (delapan) titik sudut. Kubus memiliki wujud bujur sangkar dan memiliki kata lain yaitu bidang enam yang beraturan. Contoh kubus seperti kotak kardus yang sama ukuran, dadu, dll.

Ciri-ciri bangun ruang kubus:
– Mempunyai 6 (enam) buah sisi permukaan
– Mempunyai 12 (dua belas) rusuk
– Mempunyai 8 (delapan) buah titik sudut
– Rusuk kubus sama panjang
– Sisi kubus berbentuk persegi
– Panjang diagonal ruang mempunyai ukuran yang sama
– Bidang diagonal masing-masing kubus berbentuk persegi panjang

Rumus menghitung bangun ruang kubus:
Menghitung Volume Kubus (V) = s × s × s
Menghitung Luas permukaan Kubus (L) = 6 × (s × s)

 

• Balok

Bangun Ruang Balok

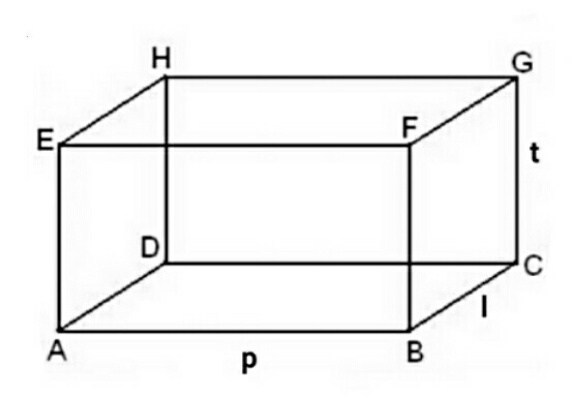
Bangun ruang balok adalah suatu bangunan ruang tiga dimensi yang dibatasi oleh 2 (dua) buah persegi dan 4 (empat) buah persegi panjang yang saling tegak lurus. Berbeda dengan kubus yang bentuk sisinya kongruen berbentuk persegi empat, balok memiliki sisi yang berhadapan sama besar ukurannya. Contoh balok di dalam kehidupan kita adalah kotak pensil, lemari pakaian, lemari pendingin, dll.

Ciri-ciri bangun ruang balok:
– Sisi balok memiliki dua pasang berbentuk persegi panjang
– Rusuk-rusuknya sejajar mempunyai panjang yang sama seperti : AE = BF= CG = DH dan AB = CD = EF GH
– Masing-masing diagonal pada bidang sisi yang berhadapan berukuran sama panjang seperti : ABCD = EFGH, ABFE = DCGH, BCFG = ADHE yang memiliki ukuran sama panjangnya.
– Masing-masing diagonal berbentuk persegi panjang

Rumus menghitung bangun ruang balok:
Rumus menghitung Volume Balok (V) = p × l × t
Rumus Luas permukaan Balok (L) = 2 × ( pl + lt + pt)

 

 Menghitung Luas permukaan Kubus (L) = 6 × (s × s)

 

• Balok

Bangun Ruang Balok

Bangun ruang balok adalah suatu bangunan ruang tiga dimensi yang dibatasi oleh 2 (dua) buah persegi dan 4 (empat) buah persegi panjang yang saling tegak lurus. Berbeda dengan kubus yang bentuk sisinya kongruen berbentuk persegi empat, balok memiliki sisi yang berhadapan sama besar ukurannya. Contoh balok di dalam kehidupan kita adalah kotak pensil, lemari pakaian, lemari pendingin, dll.

Ciri-ciri bangun ruang balok:
– Sisi balok memiliki dua pasang berbentuk persegi panjang
– Rusuk-rusuknya sejajar mempunyai panjang yang sama seperti : AE = BF= CG = DH dan AB = CD = EF GH
– Masing-masing diagonal pada bidang sisi yang berhadapan berukuran sama panjang seperti : ABCD = EFGH, ABFE = DCGH, BCFG = ADHE yang memiliki ukuran sama panjangnya.
– Masing-masing diagonal berbentuk persegi panjang

Rumus menghitung bangun ruang balok:
Rumus menghitung Volume Balok (V) = p × l × t
Rumus Luas permukaan Balok (L) = 2 × ( pl + lt + pt)

• Limas

Bangun Ruang Limas

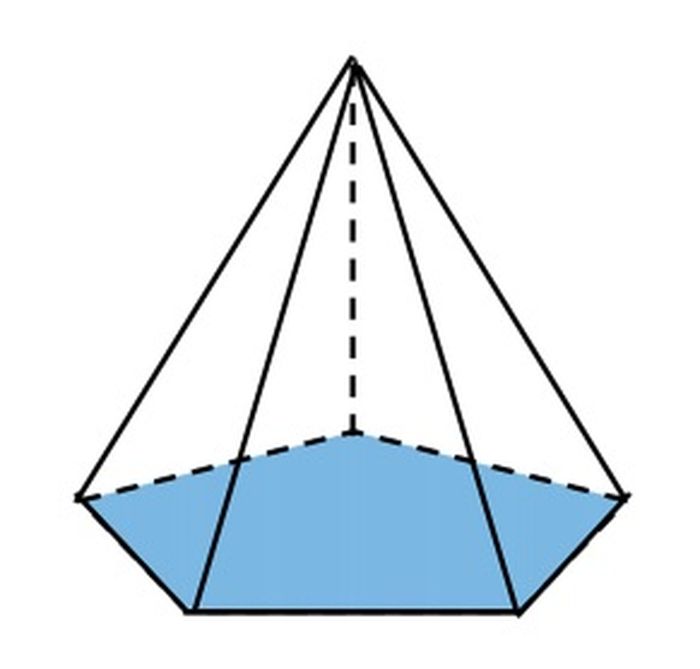
Bangun ruang limas adalah sebuah bangun ruang tiga dimensi yang dibatasi dengan alas berbentuk persegi banyak dan mempunyai sebuah titik puncak. Limas mempunyai banyak jenis seperti limas segi tiga, limas segi empat, limas segi lima, dan lain-lain. Limas dengan alas berbentuk persegi disebut piramida, sedangkan limas dengan alas berbentuk lingkaran disebut kerucut. Contoh benda limas adalah piramida di Mesir dengan alas persegi.

Ciri-ciri bangun ruang limas:
– Mempunyai 2n rusuk
– Mempunyai banyak sisi tergantung alasnya yaitu: satu sisi berbentuk persegi (bisa segi empat, segi lima, dll) berupa alas, empat sisi lainnya berbentuk segi tiga berdiri tegak dan membentuk sudut
– Mempunyai (n+1) bidang sisi
– Mempunyai (n+1) titik sudut

Rumus menghitung limas:
Rumus menghitung volume Limas (V) = 1/3 × p × l × t
Rumus menghitung luas permukaan Limas (L) = luas alas + luas selubung limas